Au plan structurel, alors qu'un graphe de fluence n'est constitué que de noeuds et d'arcs, un réseau de PETRI fera apparaitre deux catégories de noeuds:

        -  Les  places               (Pi, symbolisées par des cercles)
        -  Les  transitions        (Ti, symbolisées par des rectangles)

On dit ainsi d'un RdP que c'est un "graphe biparti" ou encore un graphe places-transitions.

Selon les circonstances, et dès lors qu'il ne peut y avoir d'ambiguités, ou que la complexité de la représentation ne l'impose pas, les transitions pourront ètre représentées par de simples barres.
 

Les arcs

Places et transitions sont reliées par des arcs. Tout arc a pour obligation de ne relier qu'une place à une transition ou une transition à une place  (figure). Un arc ne pourra jamais relier deux noeuds d'une mème catégorie.

Poids d'un arc :

A tout arc est associé un poids  n (n pris dans l'ensemble des entiers naturels).  Si ce poids n'est pas rappelé à hauteur de l'arc il sera considéré par défaut comme valant  1.

Exemple d'un réseau à arcs pondérés:

Réseau ORDINAIRE

L'arc de poids n = 1  est un arc ordinaire.

Si tous les arcs d'un réseau sont ordinaires le réseau sera dit ORDINAIRE. Les comportements  d'automates sont souvent modélisés par des réseaux ordinaires.
 

a) concernant les transitions :

Noeuds ET

JONCTION
         Deux ou plusieurs arcs aboutissant à une mème transition constituent, avec cette transition, une jonction.

DISTRIBUTION

Deux ou plusieurs arcs partant d'une mème transition constituent une distribution.
Jonctions et distributions sont des noeuds ET.

b)   concernant les places :

Noeuds OU

ATTRIBUTION
         Un ou plusieurs arcs aboutissant à une mème place constituent une attribution (convergence d'arcs sur une mème place).

SELECTION
         Deux ou plusieurs arcs issus d'une mème place constituent une sélection.
         Attributions et sélections sont des noeuds OU.

TRANSFERT
        Un transfert est une transition ne présentant qu'une place d'entrée et une place de sortie et dont les arcs sont des arcs ordinaires.

        Par la suite, un transfert pourra ètre considéré comme une jonction suivie d'une distribution
        (jonction et distribution limitée à un seul arc).

Notations :

         Pour une transition tj, toute place reliée à cette transition par un arc entrant ou un arc arrivant sur  tj est une place d'entrée pour cette transition ( places p3  et  p4   pour t3  sur le réseau       ). L'ensemble des places d'entrée d'une transition  tj  sera notée  :       °tj

         Toute place reliée à  tj  par un arc partant de  tj  est une place de sortie. L'ensemble des places de sortie d'une transition tj  sera notée:       tj°

Marquage  d'un  réseau :

Procéder au marquage d'un réseau R c'est répartir un certain nombre de jetons ou marques dans différentes places de ce réseau. On dit alors du réseau qu'il est marqué.

Un marquage du réseau précédent:

    Un marquage consiste ainsi à associer à chacune des places p d'un réseau un entier  n (avec  n >= 0). C'est le nombre de marques dans  la place  pi de R.  Ces jetons pourront ètre symbolisés par des points dans les places. On pourra aussi noter directement la valeur  n  dans la place.

On notera  M(pi)  le marquage de la place i ou le nombre de jetons dans  pi.
 

Marquage initial d'un réseau.

A tout réseau  R  on devra associer un marquage initial, soit une répartition préalable de jetons dans les places. Le marquage initial sera noté:  M0

    Le marquage initial d'un réseau conditionne souvent pour une bonne part les propriétés ou caractéristiques de ce réseau. On accompagnera donc systématiquement tout réseau de son marquage initial, on ne s'en dispense que si il n'y a aucune ambiguité sur le marquage de départ (Souvent une place de départ ou place source).

         Définissons les règles qui permettrons, sur la base de "franchissements" de transitions (on dit aussi tirs), de modifier le marquage d'un réseau.

REGLES DE FRANCHISSEMENT DES TRANSITIONS

Conventions préalables:

Validations :

         Un arc  Pi  ---->  Tj   et de poids  n  est dit "validé" si on dénombre une quantité de jetons dans la place Pi au moins égal à  n . Soit si :
                                                                                             M(pi)  >=   n

         Une transition  tj  est validée ou "franchissable" si tous ses arcs d'arrivée sont individuellement validés. On dit aussi de cette transition qu'elle est "sensibilisée" ou encore susceptible d'ètre "mise à feu" .

Réseau (        ), la transition  t   est validée, la transition t  ne l'est pas (arcs p1,t2  et  p3, t2 non valides). Réseau (       ), et pour le  marquage proposé, seule la transition t2  est validée.
 

Franchissement d'une transition :

         Si une transition t est validée, on peut déclencher une procédure de franchissement de cette transition (tir,  mise à feu). Ce franchissement s'effectue en deux étapes indivisibles.

         1' ) Dans chacune des places d'entrée  pi  de la transition on enlève  n  marques si  n est le poids de l'arc   pi ---> t.
         2' ) Dans chacune des places de sortie  pj, on place  m  marques si  m  est le poids de l'arc  t ---> pj.

Illustration :

Réseau (RdP 07), les transitions t3, t4 et t1 sont franchissables. Si nous décidons de franchir t1. Son franchissement s'opére en deux temps .

     - Retrait des jetons dans les places d'entrée de t1.
     - Rajout des jetons dans les places de sortie de t1.

(Ce conformément aux indications de poids associées aux arcs. Ces deux opérations effectuées en séquence restent indivisibles)

 Sur le réseau précédent, le  franchissement de la transition  t1. amène le marquage  M1.
 

Représentations matricielles:

Notation :
                    t1
         M0  -------> M1  ou encore :           M0   (t1   >   M1        (M0  transition t1  amène M1)

La condition pour qu'une transition  t  soit franchissable s'écrit: Quel que soit p,

                          M(p)   =>   PRE(p, t)

qui se généralise à l'ensemble des places d'entrée de la transition   t  sous la forme :

                          M  =>  PRE(t)
 

Séquence de franchissements:
 

Une suite S  de franchissements des transitions ti, tj, tk dans cet ordre sera notée   S  =  ti,  tj,  tk
On pourra trouver dans une mème séquence S de franchissements la répétition d'une mème transition t si cette transition doit ètre franchie plusieurs fois successivement avant franchissement des autres transitions. Une séquence de franchissements peut ètre légale ou pas. Pour le RdP (      ), la séquence  S =  t2, t1, t3, t4  n'est pas légale puisque le franchissement des transitions dans cet ordre est impossible. La transition t3 fait obstacle.

Graphe d'états   (G.E)

Un RdP ordinaire constitué uniquement de noeuds OU (Noeuds qui ne sont que des attributions ou des sélections) est un graphe d'états. On ne peut rencontrer dans un RdP à caractéristique de graphe d'états ni jonction ni distribution (C'est un RdP sans noeuds ET). Ce graphe s'apparente maintenant à un graphe constitué d'une seule catégorie de noeuds (les places). Les transitions devenant les arcs  interconnectant ces noeuds. C'est l'équivalent, quant à sa structure, du graphe de FLUENCE.
 

Graphe de transition d'état    (G.T.E )

         Un graphe d'état dont le marquage initial M0 ne fait apparaitre qu'un jeton et un seul est un graphe de transition d'état. Ce graphe ne contiendra plus par la suite, et quelles que pourraient ètre les séquences de franchissements, qu'un seul et mème jeton. On dit alors que le jeton est conservatif. Un tel graphe conduit souvent à la matérialisation d'une machine dite machine d'états (state machine) concue autour d'un registre d'ETAT.
 

Réseau VIVANT

         Un réseau est VIVANT, pour un marquage initial  M0  donné,  si pour toute transition  ti  et quel que soit le marquage  ultèrieur Mk  appartenant à  Q(M0), il existe une séquence légale de franchissements à partir de  Mk  contenant  ti. En d'autres termes, il sera toujours possible de repasser par le franchissement de la transition  ti.
 

Réseau SAUF

         Pour un marquage initial  M0  donné, un réseau ordinaire est sauf si il est borné à  1. Aucune de ses places n'est susceptible de contenir plus d'un jeton à la fois quel que soit le marquage atteint du réseau.
 

Réseau  CONFORME

         Un réseau est "conforme" si il est  VIVANT  et  SAUF.

Cette propriété sera souvent exigée des modèles de représentation des cahiers des charges des automatismes logiques.
(Exemple de réseau non conforme)

Réseau  PROPRE

         Un réseau est propre pour un marquage initial  M0 si, quel que soit le marquage  Mi appartenant à  Q(M0),  il existe une séquence de franchissements permettant de retrouver le marquage  Mi.

         Le réseau  (     ) emprunté à Valette  ( VAL 1 ) n'est pas propre pour  M0 = (1, 3). Son graphe des marquages conséquents (     ) suffit à le prouver par la présence du marquage (1, 3) qu'on ne peut plus retrouver ultèrieurement.
 
 
 
 

RESEAU  PUR

    Boucle élémentaire :

 Lorsqu'une place est simultanément  place d'entrée et place de sortie pour une mème transition, nous avons à faire à une boucle élémentaire (fig    ).

Un réseau est pur s'il ne fait apparaitre aucune boucle élémentaire. Ou encore si pour toute transition  t  de ce réseau on vérifie:
                                      °t  ^   t°  =   0          (vide)        ^  :  intersection
On pourra toujours représenter un réseau pur par sa matrice d'incidence.

Réseau  Libre choix

Dans un réseau libre choix, tout arc partant d'une place ne peut ètre que:
     - L'unique sortie de cette place
     - Ou l'unique entrée de la transition   (OU inclusif)
 

Réseau BORNE

         Pour un marquage initial  M0  donné, une place  p  est bornée si, pour tout marquage futur à partir de ce marquage M0, le nombre de jetons dans p n'excede jamais un nombre donné B. On peut dire aussi: Quel que soit M appartenant à la classe des marquages conséquents de M0 on aura toujours M(p) < B.

              M    Q(M0)        M(p)  <  B      avec  (B appartenant à   N )

         Un réseau est dit borné pour un marquage initial  M0  donné si toutes ses places le sont pour ce marquage initial.

    Pour le marquage initial précisé, le réseau (      ) est borné (B = 1). Le réseau (      ) n'a pas de borne. Il y a en effet accumulation de jetons possible en place (      ).
 

Réseau CONSISTANT

        Un réseau vivant et borné est un réseau consistant.

CONFLIT

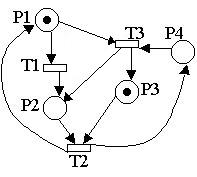
On dit qu'il y a partage d'une place  Pi  lorsque cette place est place d'entrée d'au moins deux arcs aboutissant à des transitions différentes qui sont elle-mèmes des jonctions. La place  P2  de la figure ci-après est une place partagée.

P2 introduit un "conflit". Pour le marquage P1, P2, P3, les deux transitions sont franchissables, se pose le problème de déterminer laquelle des deux transitions devra ètre franchie la première? (Rappelons que dans un RdP une opération de franchissement est une opération indivisible).
 
 

N.B:

Il faudra toujours accorder une attention particulière aux cas de conflit dans un réseau. Tout outil d'analyse, de simulation ou de de synthèse de RdP devra signaler les présences de conflits et demander à ce que ceux-ci soient régler, résolus ou spécifiés. On peut ètre amené par exemple, à décider d'une hiérarchie entre les transitions concernées et à affecter par exemple une priorité  (T1 > T2 ). On s'oblige ainsi à procéder au franchissemnt de  T1  d'abord puis à celui de  T2  si cette transition reste encore franchissable après le franchissement de  T1.

Nous verrons plus loin (Systèmes séquentiels) que nous pourrons aussi spécifier des conditions supplémentaires sur les évènements que nous serons amenés à associer aux transitions. Ainsi, dans le cas (     )  l'intersection des événements logiques  u  et   /u . v   étant nul, il ne peut pas y avoir de franchissement simultané.

Nous rencontrerons aussi des conflits au plan structurel du réseau mais ne posant pas de problème si on tient compte du marquage initial et de l'ensemble des marquages atteignables    (fig        ).
 
 

Graphe DES MARQUAGES CONSEQUENTS
 

L'ensemble des marquages atteignables (accessibles) à partir d'un marquage  Mi  sera appelé  classe des marquages conséquents de Mi  et noté:   Q(Mi)

     Pour un réseau ordinaire et conforme, on peut  représenter l'ensemble de ces marquages atteints sous forme d'un graphe dit "graphe des marquages conséquents de Mi". Le graphe obtenu a alors les caractéristiques structurelles d'un graphe d'états. Chacun des états de ce nouveau graphe, qui est un graphe de fluence ordinaire, rend compte d'un état de marquage du réseau en particulier.

N.B:  On ne peut construire le graphe des marquages conséquents d'un réseau, à partir de son marquage initial M0, que si ce réseau est borné.
 

MACRO-PLACE

Dans l'esprit d'une conception descendante hiérarchisée, on allège une représentation conprenant un grand nombre de places en en regroupant certaines dans une seule et mème place. C'est une macro-place.

- Dans le cas d'un RdP ordinaire, la délimitation de la collection de places susceptibles de constituer une macro-place devra se faire en s'assurant que de chacune des entrées dans la macroplace on peut atteindre n'importe laquelle des sorties de cette macro-place.

- On entre dans une macro-place par des arcs d'arrivée sur des places. On sort d'une macro-place par des arcs de sortie de places, donc des arcs d'arrivée sur des transitions extérieures à la macro-place. Le découpage en pointillés sur le réseau  (     )  ne saurait constituer une macro-place.

Ce n'est qu'en respectant ces conditions que l'on conserve la possibilité de procéder aux analyses des propriétés du réseau représenté cette fois au niveau macro-places.

Les macro-places participeront pour une part à la modélisation hiérarchisée des graphes de controle. La macro-place représente alors toute une activité qui n'a pas lieu d'ètre détaillée au niveau de représentation ou on se situe.
 

MACRO-TRANSITION

La forme duale de la macro-place est la macro-transition. On peut regrouper un certain nombre de places et de transitions dans une seule et mème macro-transition. L'exemple proposé figure (     ) est emprunté à PETERSON   (Computing surveys, Vol 9, N°3, sep 1987).
 

Ou les durées dans un RdP.

    Une place marquée représentera souvent le déclenchement d'une activité. Cette activité aura une certaine durée. Examinons les possibilités de représenter les durées dans un RdP.

Deux types de réseaux temporisés:

   - Les  RdP  P-temporisés
   - Les  RdP  T-temporisés

 RdP   P-temporisés

On distinguera dans un RdP   P-temporisé deux catégories de jetons:

   - Les jetons disponibles
   - Les jetons indisponibles

Le ou les jetons qui arrivent dans une place temporisée consécutivement à un franchissement sont à priori des jetons indisponibles. Ils sont indisponibles le temps de délai spécifié pour cette place. Ils ne deviennent disponibles qu'après un délai  d  spécifié pour cette place.

Toute évolution du marquage (franchissements) ne devra tenir compte que des jetons disponibles.
 

RdP  T-temporisés.

On peut attacher une durée à une transition tx. On précise qu'à partir de l'instant ou Px est marquée il y a franchissement de tx après  Ts.

Pour reprendre les conventions de  ELSIR, la durée portée à hauteur d'une transition peut ètre:

      - Une constante
      - Une  durée  aléatoire (Pouvant  ètre  fonction du ou des  jetons dans la ou les  places d'entrée de la transition (cas des réseaux colorés).
      - Fonction   du  nombre  d'opérations  exécutées  par  le  processeur  activé  par  le marquage de la place d'entrée de la transition.
      -  ....

S'il s'est agit jusqu'ici de manipulations de jetons de places en places au grès des franchissements de transitions, le besoin de disposer d'un moyen de distinguer ces jetons les uns des autres s'est vite manifesté. Le jeton est en fait lui-mème porteur d'information. Sont apparus alors les réseaux colorés (JENSEN). La coloration des jetons va enrichir les possibilités de représentations des RdP tout en réduisant notablement dans bien des cas leurs tailles. Mais si les réseaux colorés apportent énormément au plan puissance de représentations, validations et analyse des systèmes complèxes, ils ne sont pas encore vraiment utilisés à des fins d'implémentations matérielles directes. Aussi allons nous en rappeler que brièvement les principes.
 

Principe:

Si, pour un RdP généralisé, à tout arc ne peut ètre associé qu'un nombre (c'est le poids de cet arc), à tout arc d'un RdPC sera associée une fonction. Pour un arc place/transition cette fonction précise les conditions à remplir dans la place de départ pour que cet arc soit validé. Cette fonction se rapporte à la nature des jetons (couleurs) présents dans cette place de départ.
 

Tentative de classification des RdP

A l'issue de cette introduction aux RdP, on peut tenter une classification des différents types de RdP. On distinguera:

- Les réseaux dits de niveau (1) ou réseaux ordinaires. Toute place ne peut ètre marquée par au plus un jeton et un seul.  Ces jetons sont dits "jetons booléens".
- Les réseaux de Petri de niveau (2) ou réseaux généralisés. Toute place pourra contenir un certain nombre de jetons. Les jetons sont des "entiers". Les places devant contenir N jetons seront matérialisées par des compteurs.
- Les réseaux de niveau (3) ou réseaux colorés. Les jetons sont cette fois des "jetons structurés".
 

poids

  Etablir la séquence de franchissement la plus longue avant blocage du réseau. Est-elle la seule séquence possible?

<rdp_999>  -17.06.1999-